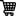Altitude of Geostationary Orbit

Important points

• The height of the geostationary orbit is 35786 kilometers above earth
• In Geostationary Orbit, the satellite moves with an orbital speed of 11068 km per hours.
• A minimum of three satellites are needed to cover the entire earth
• Super synchronous orbit is a disposal / storage orbit above GSO. From earth, they would seem drifting in westerly direction.
• Sub synchronous orbit is a orbit close to but below GSO and is used for satellites undergoing station, changes in an eastern direction.
  

For circular motion of a planet, the condition is that:

F (Gravitational) = F (centripetal)

V is the speed. Now, we know that the speed v of the planet in its orbit is equal to the circumference of the orbit divided by the time required for one revolution T. so v=2πr/T. So, the above formula becomes as follows:

From the above formula, we can derive the value of T²
as follows

The above mathematical derivation is suitable for circular as well as elliptical orbits. Now we know that geostationary satellite follows a circular, equatorial, geostationary orbit, without any inclination, so we can apply the Kepler’s third law to determine the geostationary orbit. Since, the path is circle, its semi-major axis will be equal to the radius of the orbit.

Now, it has already been calculated that Earth completes one rotation on its polar axis in 23 hr 56 min and 4.09 sec, which comes out to be 86164.09 seconds. So, the period of rotation of the Geostationary satellite should be 86164.09 seconds.

This means that

T=86164.09 seconds

Now we use this formula:

The above derivation gives the height of the Geostationary orbit. Now, please note that the above height includes radius of Earth which is 6,384 km. When we deduct it from the calculated height we get 35916 Kilometers. The precise height is altitude of 35,786 km (22,236 mi) above ground.

Orbital speed (how fast the satellite is moving through space) is calculated by multiplying the angular speed by the orbital radius:

Orbiting at the height of 22,282 miles above the equator (35,786 km), the satellite travels in the same direction and at the same speed as the Earth’s rotation on its axis, taking 24 hours to complete a full trip around the globe. Thus, as long as a satellite is positioned over the equator in an assigned orbital location, it will appear to be “stationary” with respect to a specific location on the Earth.