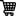A pipe can fill a tank in x hours and another can empty it in y hours. In how many hours they can together fill it (where y > x) :
A pipe can fill a tank in x hours and another can empty it in y hours. In how many hours they can together fill it (where y > x) :
[A]$latex x-y\ hours$
[B]$latex y-x\ hours$
[C]$latex \frac{xy}{y-x}\ hours&s=1$
[D]$latex \frac{xy}{x-y}\ hours&s=1$
$latex \frac{xy}{y-x}\ hours&s=1$
When both pipes are opened simultaneously, part of the tank filled in 1 hour
$latex = \frac{1}{x}-\frac{1}{y}=\frac{y-x}{xy}&s=1$
∴ Required time $latex = \frac{xy}{y-x}\ hours&s=1$
Hence option [C] is correct answer.
