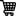The number of terms in the series 1 + 3 + 5 + 7 + …. + 73 + 75 is :

38
Let the number of terms be n.
It is an Arithmetic Series whose first term, a = 1 and common difference d = 2.
∴ n^th term = a + (n – 1) d
$latex => 75 = 1 + (n – 1) 2&s=1$
$latex => 2 (n – 1) = 74&s=1$
$latex => n – 1 = \frac{74}{2} = 37&s=1$
$latex => n = 37 + 1 = 38&s=1$
Hence option [C] is the right answer.