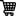Twelve Yantras of Lalla

Lalla was an Indian astronomer and mathematician who followed the tradition of Aryabhata I. Lalla’s most famous work was entitled Shishyadhividdhidatantra. He was well known because of twelve instruments which he brought into practice. One of the most discussed shloka of Lalla is as follows:

In the above Shloka, Lalla describes the 12 Instruments as follows:

Sphere, ring, dial, bow, time measuring water vessel, Gnomon, divider, scissor. Circular seat with central stick, semicircle with stick, combination of sticks, are the twelve instruments along with a stick.

The 12 instruments are as follows:

1. The Gola yantrais a type of armilliary sphere used to locate planetary positions.
2. Bhanganais a ring with angular graduations alonge its circumference, it is a type of protractor.
3. Chakrais a circular disk with angular graduations; it is also a type of protractor.
4. Dhanuis a semicircular disk with angular graduations and a stick pivoted at the center, it is a type of protractor with a plumb bob arrangement.
5. Ghati is a small vessel with a hole at the bottom. It was used to measure time.
6. Shankuis a type of gnomon, a long vertical cone used to identify East-West-North-South direction based on shadow of its tip.
7. A special geometrical construction known a ‘Matsya‘ was used for the above purpose. Altitude of sun and day time was also measured with this instrument based on the shadow.
8. Shakata consists of two ‘V’ shaped sticks, pivoted at the end.
9. Kartari means a seizer. This instrument is made up of two sticks both pivoted together. It was used like a caliper, and also to measure angle with the help of protractor.
10. Pithais a horizontal disk with a vertical stick at its center. It was used to measure local time based on its shadow, it was used to measure the height with the help of special geometrical contruction.
11. Shalakais combination of two sticks with a string.
12. Yasti is just a long stick having standard dimensions; it was used to measure height and distances. Special geometrical constructions were framed to facilitate the use of this stick. These proposed geometrical constructions were to construct the proportionate triangles with the help of which heights of terrestrial objects could be calculated.